Graph Signal Sampling for Inductive One-Bit Matrix Completion: a Closed-form Solution

Abstract

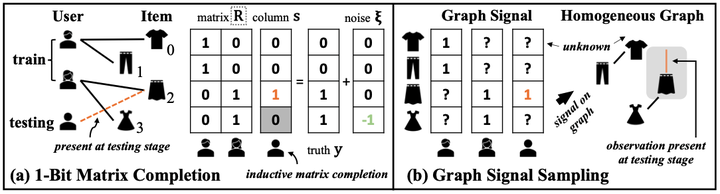
Inductive 1-bit matrix completion is motivated by modern applications such as recommender systems, where new users would appear at test stage with the ratings consisting of only ones and no zeros. We propose a unified graph signal sampling framework which enjoys the benefits of graph signal analysis and processing. The key idea is to transform each user’s ratings on the items to a function (signal) on the vertices of an item-item graph, then learn structural graph properties to recover the function from its values on certain vertices — the problem of graph signal sampling. We propose a class of regularization functionals that takes into account discrete random label noise in the graph vertex domain, then develop the GS-IMC approach which biases the reconstruction towards functions that vary little between adjacent vertices for noise reduction. Theoretical result shows that accurate reconstructions can be achieved under mild conditions. For the online setting, we develop a Bayesian extension, i.e., BGS-IMC which considers continuous random Gaussian noise in the graph Fourier domain and builds upon a prediction-correction update algorithm to obtain the unbiased and minimum-variance reconstruction. Both GS-IMC and BGS-IMC have closed-form solutions and thus are highly scalable in large data. Experiments show that our methods achieve state-of-the-art performance on public benchmarks.